[Paper Review & Experiment] Entity Embeddings of Categorical Variables
다소 개인적인 의견이 반영되어있고, review를 목적으로 작성된 글입니다. 문제가 된다면 글을 내리도록 하겠습니다.
Prologue
본인은 최근에 정형 데이터(structured data or tabular data)를 활용하여 우범여부, 다시 말해 이진분류(binary classification)의 문제를 해결하려는 시도를 했다. 글을 작성하는 시점을 기준으로 최근 Tabular Data: Deep Learning is Not All You Need 라는 preprint가 업로드 되었고, 결론만 말하자면 ensemble 기반의 모델인 XGBoost 를 사용하는 것이 전반적인 대부분의 요소를 고려할 때 다른 인공신경망(neural network, NN)을 굳이 사용하지 않더라도 좋은 성능을 보일 수 있다는 내용을 담고 있다.
실제로 첫 시도는 tabular data 내에 포함된 범주형 변수(categorical variables)에 대하여 전부 one-hot encoding을 적용하여 XGBoost 모델의 input data로 사용하였다. 수치형 변수(numerical variables)에 대한 전처리 또한 완료한 상태이다. 불균형 데이터(imbalanced data)임을 고려하여 AUC 지표를 활용하여 성능을 평가하는데, 어느 정도의 한계를 넘지 못하였고 그 이유는 categorical variables의 cardinality와 관련이 있다고 판단하였다.
먼저 one-hot encoding을 사용하여 새롭게 생성되는 tabular data는 Figure. 1을 예제로 살펴 볼 수 있다. Cardinality는 집합의 크기를 표현하는 원소 개수에 대한 척도이다. Figure. 1의 blood type의 경우 기존의 tabular data의 column(or feature)에서 확인할 수 있는 요소는 중복을 제거하고 3개의 유일한 원소를 확인할 수 있다. 즉, B를 해당 table 내의 blood type의 집합이라고 한다면 |B| = 3 이라고 표현할 수 있다.

Feature의 cardinality가 크다면 one-hot encoding과 같은 방법을 사용할 때 차원(dimension)이 그 만큼 커짐을 직관적으로 이해할 수 있다. 그리고 table의 값들은 희소(sparse) 형태를 가지게 되는데, 이 encoded table을 그대로 활용하는 것에는 몇 가지 단점을 수반한다. 첫 번째는 컴퓨터 메모리 용량이 충분하지 않을 경우 실험조차 불가능하다. 두 번째는 늘어난 dimension을 활용하여 task를 수행할 때, 모든 feature가 전부 유용하게 쓰인다고 보장할 수 없고, 일부는 성능 저하의 원인이 될 수 있다. 때문에 필자의 사전지식을 바탕으로 이를 해결하기 위한 방법이 두 가지 정도 있을 것이라 생각했다.
1. feature selection
2. dimension reduction (using embedding)
이 중에서 필자는 2번, 구체적으로 embedding을 사용하여 시도해 보았다. 실험에서 해당 글의 제목인 Entity Embeddings of Categorical Variables 이라는 preprint 논문의 아이디어를 참고하였고, 몇 가지 다른 방식과 성능을 비교하였다. 결국 본인은 Neural network 기반의 embedding 방법이 tabular data내에 high cardinality를 가지는 feature들이 존재할 때, 효과적으로 의미를 함축하고 성능을 개선할 수 있을 것인가에 대한 궁금증을 해결하려고 하였다.
Introduction
저자는 비정형 데이터(unstructured data)를 다룰 때와 달리, kaggle과 같은 대회에서 structured data를 다룰 때 상위 팀들이 tree 계열의 방법론을 자주 사용하는 경향이 있었다고 언급한다. 그리고 continuity라는 데이터 속성에 대하여 이야기하는데, 데이터의 continuity를 통해 우리는 NN의 power를 증가시킬 수 있다고 주장한다. 예시로 Convolutional neural networks(CNN)가 flattened vector가 아닌 인접한 pixel 간의 정보를 고려할 수 있게 되었다는 점과 자연어처리 분야에서 word embedding이 word space 내에서 배치될 때 유사한 정도에 따라 그 거리가 결정되어 one-hot encoding과 같은 방식보다 continuity를 고려할 수 있었다는 점을 제시한다. 하지만 categorical features을 가지는 structured data는 continuity을 고려할 수 없을 가능성이 존재하고, 있어도 명확하지 않을 수 있다고 주장하고 활자 그대로 인용하여 아래와 같이 지필하였다.
The continuous nature of neural networks limits their applicability to categorical variables.
(신경망의 continuous nature는 범주형 변수에서 그 적용 가능성이 제한된다.)
Therefore, naively applying neural networks on structured data with integer representation for category variables does not work well.(그래서, 작동이 잘 안된다.)
이를 위한 간단한 해결책으로 one-hot encoding을 사용할 수 있지만, 아래와 같은 두 가지 문제점을 함께 제시한다.
First, when we have many high cardinality features one-hot encoding often results in an unrealistic amount of computational resource requirement.
Second, it treats different values of categorical variables completely independent of each other and often ignores the informative relations between them.
그래서 저자는 entity embedding을 통해 multi-dimensional spaces에서 categorical features의 representation을 자동으로 학습하면서 데이터의 intrinsic continuity을 드러낼 수 있는 아이디어를 제안한다.
Related Work & Tree based Methods
이 section에서는 기존의 unstructured data에서 embedding 을 위한 사전기술에 대한 언급과 single decision tree 와 ensemble 방법에 대한 간단한 서술이 포함되어 있다. (자세한 내용 생략)
Structured Data
위에서부터 필자가 계속 언급한 structured data가 무엇인가 서술하고 이에 제한하여 해당 section의 내용을 설명할 것을 밝힌다. structured data에서 가장 일반적인 형태로 크게 continuous variables와 discrete variables가 있고 discrete variables에서 integer로 표현 가능한 것에 대하여 nominal numbers과 ordinal numbers(or cardinal number)로 구분하여 예시를 들어 설명한다. 이 둘은 integer 값에 따라 순서의 의미를 내재하는지에 따라 구분되는 개념으로 저자는 두 유형에 대하여 동일한 방식으로 처리하기 위한 entity embedding을 제안하며, 유사한 의미를 내재한다면 multi-dimensional space에서 가까운 위치에 mapping 될 것이라고 언급한다.
Entity Embedding

Figure. 2는 저자가 제안하는 entity embedding을 위한 NN 구조이다. 그림을 통해 직관적으로 이해할 수 있는 정보는 각 feature에 대한 embedding을 다르게 수행하여 'dense layer 0'에서 그 정보를 concatenation하는 구조라는 것이다. 논문에서 서술한 흐름을 그대로 따라가보면 우선 discrete variable의 각각에 대하여 embedding을 위한 mapping이 요구되어 아래와 같이 약식으로 표현한다.

이는 mapping에 대한 입력(scalar format)과 출력(vector format)만을 표현하고 구체적으로 Kronecker delta를 언급하여 구체적으로 서술한다. 링크를 따라 들어가면 그 의미를 쉽게 이해할 수 있는데 그 정의는 아래와 같다.

즉, 0과 1로 그 값을 정의할 수 있는데 두 정수가 같다면 1, 다르다면 0이 된다. 이 정의를 먼저 이해하고 논문에서 언급한 다음 수식을 보면 이해가 쉽다.
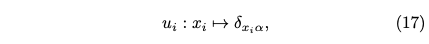

If m_i is the number of values for the categorical variable x_i, then δ_xiα is a vector of length m_i, where the element is only non-zero when α = x_i.
β는 embedding layer의 index를 의미하고 w_αβ 는 one-hot encoding layer와 embedding layer 사이의 weight를 의미하는 요소로 식(16)의 출력 x를 결정하는 구체적인 수식표현이다. 그리고 Figure. 2의 EE layer를 위한 dimension의 크기는 hyperparameters로 feature 마다 원래 cardinarity를 기준으로 1씩 크기를 줄이면서 적정 값을 찾는 empirical guideline을 제시한다.
Experiments
저자는 kaggle의 rossmann-store-sales 데이터를 사용하여 회귀(regression) 문제를 해결하기 위한 다양한 비교 실험을 결과로 보인다. 자세한 결과 비교는 생략하고 해당 section에서는 본인의 실험 내용을 정리해본다. (저자의 실험결과 참고 논문)
본인이 실험에서 비교한 모델의 구조는 Figure. 3-4의 좌상단에 보이는 기본적인 NN 구조와 비교를 위한 두 가지 모델이다. 하나는 Figure. 3에서 보이는 Autoencoder를 사용하여 비지도학습(unsupervised learning) 기반의 방법으로 잠재 벡터(latent vector)를 얻어 기본적인 NN 구조의 입력으로 활용하는 것. 둘은 Figure. 4에서 보이는 논문에서 제안하는 entity embedding의 구조를 활용한다.


나머지 조건은 가능한 동일하게 설정(model의 capacity 등)하고 실험하여 우범여부 분류에 대한 평가 지표로 정확도(accuaracy)와 AUC 값을 비교하였다. Label이 5:1 비율로 존재하는 상황에서 5-fold cross validation을 통해 확인한 결과 처음 xgboost 방식을 적용하였을 때 accuaracy 와 모든 방법에 차이가 소수점 두번째 자리에서 근소하게 발생하였다. 비교한 방법들 사이의 성능이 비슷해 보이지만 AUC 지표로 비교하였을 때 NN 기반의 모든 방식(NN baseline과 Figure. 3-4 의 모든 방식)이 xgboost 방법을 사용하였을 때보다 0.1 정도의 높은 점수를 보이고 NN 계열 내에서는 극적인 차이를 보이지 않았다는 것이 결론이다.. ;ㅁ;
Future Work
아무래도 preprint이라서 그런지 저자는 시간 관계상의 한계로 인해 추가적으로 고려해야할 것들이 몇 가지 있다고 밝힌다.
First of all, entity embedding should be tested with more datasets, in particular datasets with many high cardinality features, where the data is getting sparse and entity embedding is supposed to show its full strength compared with other methods. For some datasets and entity embeddings it could also be interesting to explore the meaning of the directions in the embeddings like those in Eq. (2) and Eq. (3).
Second, we only touched the surface of the relation of entity embedding with the finite metric spaces. A deeper understanding of this relation might also help to find the optimal dimension of the embedding space and how neural networks work in general.
Third, similar methods may be applied to improve the approximation of continuous (i.e. non-categorical), but non-monotone functions. One way to achieve this is by discretizing the continuous variables and transform them into categorical variables as discussed in this paper.
Last, it might be interesting to systematically compare different activation functions of the entity embedding layer.
첫 번째에 대하여 본인이 실험한 결과를 통해 제안하는 방법이 유효한지 아직 판단할 수 없다는 것을 깨달았다. 본인이 실험에서 사용한 데이터의 경우 하나의 feature에 대한 cardinality가 1000이 넘는 경우를 포함하고 이와 비슷한 수준으로 cardinality가 큰 column이 대부분인 데이터 통해 실험을 진행한 것이다.
Epilogue
Entity embedding을 설명한 section에는 이 글에서 언급하지 않은 subsection이 포함되어 있는데, 그것은 유한거리공간(finite metric space)을 고려하여 작성된 내용이다. 저자는 embedding을 통해 categorical variable의 유사한 값을 embedding space 내에서 가까운 위치에 존재할 수 있도록 하려는 의도를 서술한다. 그리고 이것은 위상수학(topology)에서 finite metric space problem과 연관성이 있다고 한다. finite metric space를 categorical variable x_i와 연관짓고 (M_i, d_i)라 정의 내린다. M_i는 x_i의 가능한 모든 값의 집합이고, d_i는 두 x_i 사이의 거리 함수라고 할 때, d_i는 단편적으로 식(19)로 표현할 수 있다.

추가적으로 논문에서 언급하는 식(20-22)의 특성을 만족하고 Metric spaces and positive definite functions를 참고하여 euclidean metric space에 generic metric space가 isometrically embedding 된다는 필요충분조건임이 증명된 상태이다. 논문에서는 식(19)를 대입하여 생각하기 위해 아래와 같은 positive definite를 전제한다.
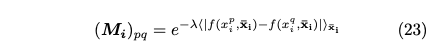
하지만 과거 입증된 이론과는 맞지 않고, 저자들이 정의한 metric space가 euclidean metric space에 isometrically embedding 되지 않음을 아래의 그림을 통해 보여준다.

그리고 아래와 같은 질문을 남기고 future work로 과제를 넘긴다.
It is not an isometric embedding obviously.
We can also see from the figure that there is a linear relation with well defined upper and lower boundary.
Why are there clear boundaries and what does the shape mean?
Is this related to some theorems regarding the distorted mapping of metric space?
How is the distortion related to the embedding dimension D_i?
If we apply multidimensional scaling directly on the metric d_i, how is the result different to the learned entity embeddings of the neural network?